mathe

 

Startseite

2012

2013

 

 

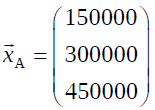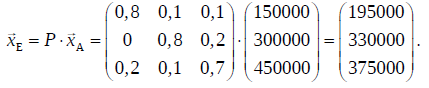
Abiturprüfung 2011

 


Aufgabenstellung:

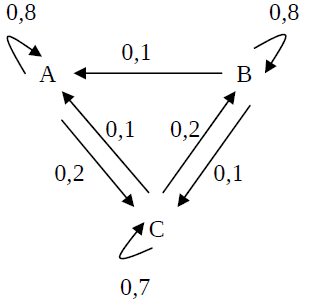
Drei Kaffeeröstereien konkurrieren mit ihren Kaffeesorten A, B und C um die Gunst der Käufer, wobei folgendes monatliche Wechselverhalten der Käufer zu beobachten ist:
20 % der Käufer der Sorte A wechseln zu Sorte C,
10 % der Käufer der Sorte B wechseln zu Sorte A,
10 % der Käufer der Sorte B wechseln zu Sorte C,
10 % der Käufer der Sorte C wechseln zu Sorte A,
20 % der Käufer der Sorte C wechseln zu Sorte B
Gehen Sie davon aus, dass die übrigen Käufer bei der gewählten Kaffeesorte bleiben und
sich das Wechselverhalten über längere Zeit nicht ändert.


a) Skizzieren Sie das monatliche Wechselverhalten der Käufer in einem Übergangsdiagramm
und beschreiben Sie, inwiefern die Übergangsmatrix

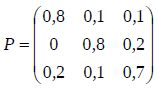
das dargestellte Wechselverhalten der Käufer abbildet. (8 Punkte)

Verstecktes Layer sichtbar machen Lösung



b) Berechnen Sie die Verteilung nach einem Monat, wenn vorher 150 000 Sorte A, 300 000 Sorte B und 450 000 Sorte C gekauft haben. (4 Punkte)

Lösung



c) Berechnen Sie P2 und interpretieren Sie die Komponente in der dritten Zeile und ersten Spalte sowie die Komponente in der dritten Zeile und dritten Spalte von P2 im Sachzusammenhang. (6 Punkte)

Lösung



d) Die Matrix P aus Teil a) hat die besondere Eigenschaft, dass alle Komponenten größer oder gleich Null sind und alle Spalten die Summe 1 haben. Eine solche Matrix wird stochastisch genannt.
Interpretieren Sie diese Eigenschaft im Sachzusammenhang und beurteilen Sie die Angemessenheit der dahinter liegenden Modellannahme für das Wechselverhalten der Käufer zwischen den drei Kaffeesorten. (6 Punkte)

Lösung




Eine weitere Kaffeerösterei bietet eine vierte Kaffeesorte D an. Das Wechselverhalten der Käufer wird durch die Matrix


beschrieben, wobei eine Verteilung der Käufer auf die Sorten A, B, C und D durch den Vektor


gegeben ist.




e) (1) Skizzieren Sie das monatliche Wechselverhalten der Käufer in einem Übergangsdiagramm.
(2) Bestimmen Sie für die Übergangsmatrix Q die prozentuale Verteilung der Käufer, die sich im Folgemonat nicht ändert.
Interpretieren Sie diese Verteilung im Hinblick auf das langfristige Käuferverhalten. (16 Punkte)

Lösung



f) Durch mangelnde Betreuung der Stammkunden verliert die Rösterei, die Sorte C anbietet, Käufer an die übrigen Röstereien, so dass sich die entsprechenden Übergangsquoten ändern. Alle anderen Übergangsquoten bleiben gleich.
Die Verteilung Ändert sich in einem Monat von (400 000|200 000|400 000|100 000) zu (400 000|300 000|200 000|200 000).
(1) Begründen Sie, dass dieses Verhalten durch eine Matrix des Typs


beschrieben werden kann.
(2) Ermitteln Sie die neuen Übergangsquoten.

Lösung


 
   

   © 2015 by AL •