mathe

 

Startseite

2011

2012

 

 

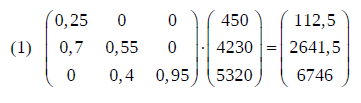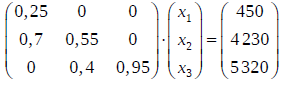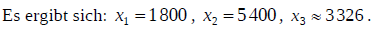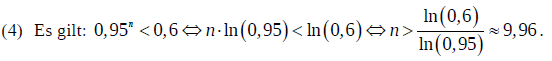
Abiturprüfung 2013

 


Aufgabenstellung:

Von einem Forstbetrieb werden auf verschiedenen Waldflächen Tannen gezogen. Entsprechend ihrer Höhe werden die Tannen in drei Größenklassen eingeteilt: Tannen, die weniger als einen Meter groß sind, gehören zur Größenklasse K (klein); Tannen, die mindestens einen Meter, aber weniger als zwei Meter groß sind, gehören zur Größenklasse M (mittel); Tannen, die mindestens zwei Meter groß sind, gehören zur Größenklasse G (groß). Jeweils zu Beginn eines festen Zeitraums (Wachstumsperiode), auf den sich im Folgenden die Übergänge zwischen den drei Größenklassen beziehen, wird eine Bestandsaufnahme durchgeführt. Die Übergangsquoten berücksichtigen, dass abgestorbene, kranke oder beschädigte Bäume im Laufe jeder Wachstumsperiode aus dem Bestand entfernt werden.


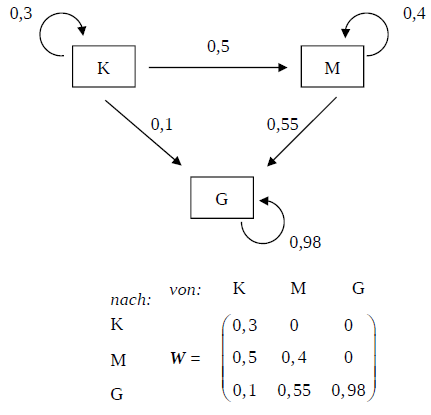
a) Auf einer der Waldflächen erreichen von den Tannen der Größenklasse K innerhalb einer Wachstumsperiode 50 % die Größenklasse M und 10 % die Größenklasse G, während 30 % in der Größenklasse K verbleiben. Von den Tannen der Größenklasse M erreichen innerhalb einer Wachstumsperiode 55 % die Größenklasse G, während 40 % in der Größenklasse M verbleiben. Von den Tannen der Größenklasse G sind am Ende einer Wachstumsperiode noch 98 % in der Größenklasse G.
Stellen Sie dieses Wachstumsverhalten durch ein Übergangsdiagramm dar und bestimmen Sie eine Übergangsmatrix, die dieses Wachstumsverhalten beschreibt. (10 Punkte)

Verstecktes Layer sichtbar machen Lösung





Auf einer anderen Waldfläche wird eine andere Art von Tannen gezogen. Eine Zählung ergab die folgende Übergangsmatrix A für das Übergangsverhalten zwischen den oben genannten Größenklassen innerhalb einer Wachstumsperiode:

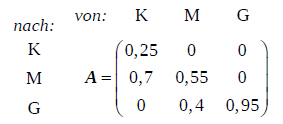
In Teilaufgabe b) wird angenommen, dass diese Übergangsquoten auch für die vorangegangenen und folgenden Wachstumsperioden gelten.



b)Die Bestandsaufnahme zu Beginn einer bestimmten Wachstumsperiode ergibt 450 Tannen der Größenklasse K, 4230 Tannen der Größenklasse M und 5320 Tannen der Größenklasse G.
(1) Bestimmen Sie die Anzahl der Tannen in den einzelnen Größenklassen am Ende dieser Wachstumsperiode.
(2) Bestimmen Sie die Anzahl der Tannen in den einzelnen Grö0enklassen eine Wachstumsperiode vor dem Zeitpunkt der Bestandsaufnahme.
(3) Zeigen Sie ausgehend von einem beliebigen Bestandsvektor

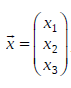
dass der Gesamtbestand an Tannen am Ende einer Wachstumsperiode 95 % des Bestandes zu Beginn dieser Wachstumsperiode beträgt.
(4) Berechnen Sie, nach wie vielen Wachstumsperioden erstmals weniger als 60 % des ursprünglichen Gesamtbestandes an Tannen vorhanden sind. (20 Punkte)

Lösung




Nun wird davon ausgegangen, dass jeweils am Ende einer Wachstumsperiode, innerhalb derer sich der Bestand zunächst gemäß der Übergangsmatrix A entwickelt hat, 56 % des dann vorhandenen Bestandes der Größenklasse G gefällt und danach genau so viele Tannen in der Größenklasse K neu gesetzt werden, wie zuvor in der Größenklasse G gefällt wurden.



c) (1) Bestimmen Sie ausgehend von einem beliebigen Bestandsvektor

zu Beginn einer Wachstumsperiode, wie viele Tannen in den einzelnen Größenklassen am Ende der Wachstumsperiode nach dem Fällen und vor dem Wiederaufforsten vorhanden sind.



(2) Gesucht ist eine Übergangsmatrix C, die den Übergang zwischen den Größenklassen K, M und G innerhalb einer Wachstumsperiode unter Berücksichtigung der abschließenden Fäll- und Wiederaufforstungsarbeiten beschreibt.
Zeigen Sie, dass

gilt.

(3) Begründen Sie, dass nach der Wiederaufforstung am Ende einer Wachstumsperiode der Gesamtbestand an Tannen 95 % des Bestandes zu Beginn dieser Wachstumsperiode beträgt.

(4) Bestimmen Sie bezogen auf einen beliebigen Bestandsvektor

zu Beginn einer Wachstumsperiode, wie viele Tannen der Größenklasse K nach den Fällarbeiten am Ende der Wachstumsperiode insgesamt neu gesetzt werden müssten, damit die Gesamtzahl der Tannen am Ende der Wachstumsperiode gleich der Anzahl der Tannen zu Beginn dieser Wachstumsperiode ist. (20 Punkte)

Lösung



 
   

   © 2015 by AL •